Differential equations and linear algebra goode – Differential Equations and Linear Algebra by Goode provides a comprehensive and engaging exploration into the fundamental concepts and applications of these mathematical disciplines. From the intricacies of differential equations to the power of linear algebra, this book offers a deep dive into the tools and techniques that shape our understanding of the world around us.
Delving into the realm of differential equations, readers will encounter the concepts of order, degree, and linearity, gaining a firm grasp of the methods used to solve these equations, such as separation of variables and integrating factors. The study of linear algebra introduces vector spaces and subspaces, along with the properties that define them.
Linear transformations and their matrices, including eigenvalues and eigenvectors, become central to understanding the applications of linear algebra in diverse fields, including computer graphics and quantum mechanics.
Differential Equations
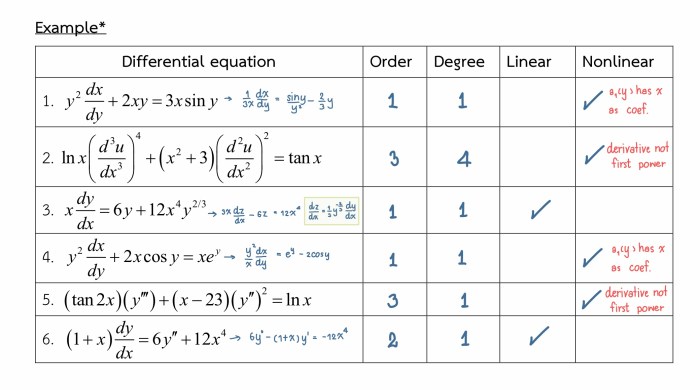
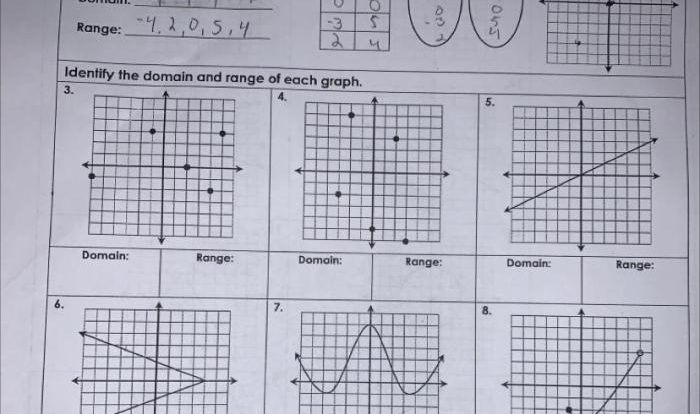
Differential equations are mathematical equations that relate a function to its derivatives. They are used to model a wide variety of phenomena, from the motion of planets to the flow of fluids. Differential equations can be classified by their order, degree, and linearity.
The order of a differential equation is the highest order of derivative that appears in the equation. The degree of a differential equation is the highest power of the derivative that appears in the equation. A differential equation is linear if it can be written in the form $a_0(x)y^(n) + a_1(x)y^(n-1) + \cdots + a_n(x)y = f(x)$, where $a_0(x), a_1(x), \cdots, a_n(x)$ are constants or functions of $x$, and $f(x)$ is a function of $x$.
There are many different methods for solving differential equations. Some of the most common methods include separation of variables, integrating factors, and Laplace transforms.
Linear Algebra

Linear algebra is the branch of mathematics that deals with vector spaces and linear transformations. Vector spaces are sets of objects that can be added and scaled. Linear transformations are functions that preserve the operations of addition and scalar multiplication.
Linear algebra has a wide range of applications in fields such as computer graphics, quantum mechanics, and economics. For example, linear algebra is used to compute the eigenvalues and eigenvectors of a matrix. Eigenvalues and eigenvectors are important for understanding the behavior of linear transformations.
Applications of Differential Equations and Linear Algebra
Differential equations and linear algebra are used to model and solve a wide variety of real-world problems. For example, differential equations are used to model the motion of planets, the flow of fluids, and the growth of populations. Linear algebra is used to solve systems of linear equations, to compute the eigenvalues and eigenvectors of a matrix, and to perform other operations on vectors and matrices.
Differential equations and linear algebra are essential tools for scientists, engineers, and mathematicians. They are used to solve a wide variety of problems in fields such as physics, engineering, and finance.
Historical Development: Differential Equations And Linear Algebra Goode
The history of differential equations and linear algebra can be traced back to the early days of mathematics. The first differential equation was solved by Isaac Newton in the 17th century. In the 18th century, Leonhard Euler developed the theory of linear algebra.
In the 19th century, differential equations and linear algebra were used to solve a wide variety of problems in physics and engineering. In the 20th century, these mathematical tools were used to develop new technologies, such as computers and nuclear weapons.
Resources for Learning
There are many different resources available for learning differential equations and linear algebra. Some of the most popular resources include textbooks, online courses, and software packages.
When choosing a resource for learning differential equations and linear algebra, it is important to consider your learning style and your goals. If you are a visual learner, you may want to choose a resource that includes lots of diagrams and illustrations.
If you are a hands-on learner, you may want to choose a resource that includes lots of practice problems.
No matter what your learning style or your goals, there is a resource available that can help you learn differential equations and linear algebra.
FAQ Overview
What is the significance of differential equations in real-world applications?
Differential equations are essential in modeling and solving problems in various fields, including physics, engineering, and finance. They allow us to describe and predict the behavior of dynamic systems, such as the motion of objects, the flow of fluids, and the growth of populations.
How does linear algebra contribute to computer graphics?
Linear algebra provides the mathematical framework for representing and manipulating 3D objects in computer graphics. It enables transformations, rotations, and projections, allowing for realistic and efficient rendering of virtual environments and animations.