Parallel lines cut by a transversal notes an intriguing intersection of geometry and algebra. Delving into this topic unveils a fascinating interplay of lines and angles, governed by a set of well-defined properties and theorems. As we embark on this exploration, we will unravel the intricacies of these geometric relationships, shedding light on their practical applications in the world around us.

The concept of parallel lines intersected by a transversal forms the cornerstone of this discussion. Parallel lines, by definition, never meet, while a transversal intersects them at distinct points, creating various angles. Understanding the properties that govern these angles, such as corresponding, alternate interior, and alternate exterior angles, is crucial for comprehending the behavior of parallel lines cut by a transversal.

Parallel Lines Cut by a Transversal

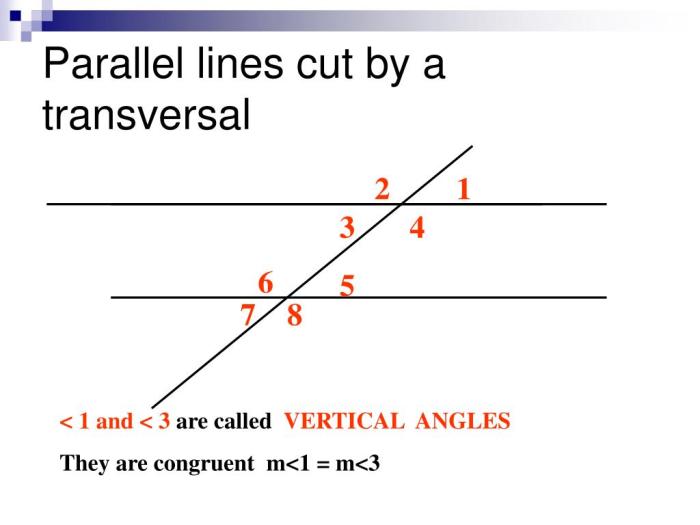
When two lines intersect a third line, the lines are called transversals. The transversals create eight angles. These angles have special relationships to each other, and these relationships are described by theorems about parallel lines cut by a transversal.

Definitions, Parallel lines cut by a transversal notes

• Parallel linesare lines that never intersect.
• A transversalis a line that intersects two or more other lines.
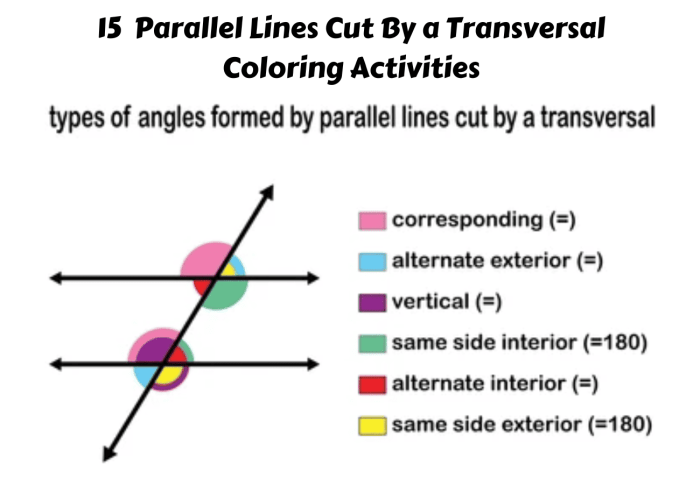
• Corresponding anglesare angles that are in the same position relative to the transversal.
• Alternate interior anglesare angles that are on opposite sides of the transversal and inside the two lines.
• Alternate exterior anglesare angles that are on opposite sides of the transversal and outside the two lines.

Properties of Parallel Lines Cut by a Transversal

Parallel lines cut by a transversal have the following properties:

• Corresponding angles are congruent.
• Alternate interior angles are congruent.
• Alternate exterior angles are congruent.

These properties can be used to prove other theorems about parallel lines.

Theorems Related to Parallel Lines Cut by a Transversal

• Angle Bisector Theorem:If a transversal bisects one of the angles formed by two parallel lines, then it bisects the other angle.
• Converse of the Angle Bisector Theorem:If a transversal bisects both of the angles formed by two parallel lines, then the lines are parallel.
• Same-Side Interior Angles Theorem:If a transversal intersects two parallel lines, then the same-side interior angles are supplementary.
• Converse of the Same-Side Interior Angles Theorem:If a transversal intersects two lines, and the same-side interior angles are supplementary, then the lines are parallel.
• Alternate Interior Angles Theorem:If a transversal intersects two parallel lines, then the alternate interior angles are congruent.
• Converse of the Alternate Interior Angles Theorem:If a transversal intersects two lines, and the alternate interior angles are congruent, then the lines are parallel.
• Alternate Exterior Angles Theorem:If a transversal intersects two parallel lines, then the alternate exterior angles are congruent.
• Converse of the Alternate Exterior Angles Theorem:If a transversal intersects two lines, and the alternate exterior angles are congruent, then the lines are parallel.

Applications of Parallel Lines Cut by a Transversal

Parallel lines can be used to find unknown angle measures. For example, if you know the measure of one angle and the type of angle it is (corresponding, alternate interior, or alternate exterior), you can use the properties of parallel lines to find the measure of the other angles.

Parallel lines can also be used to construct parallel lines. For example, if you have a line and a point not on the line, you can use a transversal to construct a line parallel to the given line that passes through the point.

Parallel lines are used in many real-world applications, such as architecture, engineering, and surveying.

Clarifying Questions: Parallel Lines Cut By A Transversal Notes

What is the relationship between parallel lines and transversals?

Parallel lines never meet, while a transversal intersects them at distinct points, creating various angles.

What are the different types of angles formed when a transversal intersects parallel lines?

Corresponding angles, alternate interior angles, and alternate exterior angles are the three main types of angles formed.

How can we use the properties of parallel lines cut by a transversal to solve problems?

These properties allow us to determine the measures of unknown angles, construct parallel lines, and solve various geometric problems.