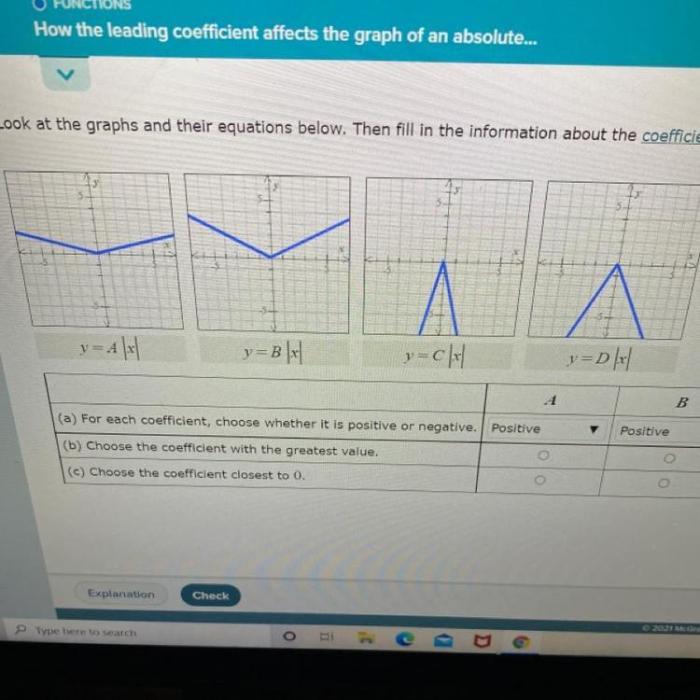
Choose the coefficient closest to 0 – In the realm of mathematical expressions, the concept of coefficients holds significant importance, as they shape the behavior of equations. Approximating coefficients to zero emerges as a valuable technique in data analysis, offering insights into trends and patterns within data sets.
This guide delves into the intricacies of choosing the coefficient closest to zero, exploring its applications and limitations.
By understanding the process of approximating coefficients to zero, we gain the ability to manipulate equations, analyze their behavior, and extract meaningful information from data. This guide serves as a comprehensive resource for anyone seeking to master this technique.
Coefficient Values
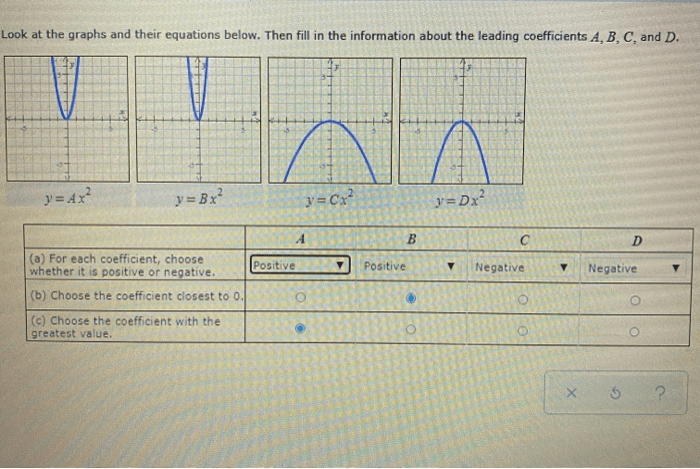
In mathematical expressions, coefficients are numerical values that multiply variables. They represent the magnitude or intensity of the variable’s contribution to the overall expression. For example, in the equation 3x + 5, the coefficient of x is 3, indicating that x is multiplied by 3. Coefficients play a crucial role in determining the behavior and characteristics of equations.
Approximating Coefficients to Zero, Choose the coefficient closest to 0
Approximating coefficients to zero involves finding the coefficient that is closest to zero while still maintaining the general behavior of the equation. This process is often used to simplify equations or to identify limiting values. One method for approximating coefficients to zero is by rounding the coefficient to the nearest integer or decimal place that does not significantly alter the equation’s behavior.
Impact on Equation Behavior
Approximating coefficients to zero can have a significant impact on the behavior of equations. For linear equations, approximating the slope coefficient to zero effectively reduces the equation to a horizontal line. In quadratic equations, approximating the coefficient of the quadratic term to zero simplifies the equation to a linear equation.
These approximations can alter the shape, intercepts, and solutions of the equations.
Applications in Data Analysis
Approximating coefficients to zero finds applications in data analysis. By approximating coefficients to zero, it is possible to identify trends, patterns, and outliers in data sets. For example, in a linear regression model, approximating the slope coefficient to zero indicates that there is no significant linear relationship between the independent and dependent variables.
Limitations and Considerations
While approximating coefficients to zero can be a useful technique, it is important to consider its limitations. Approximations may introduce errors or inaccuracies, especially when the coefficients are small but not negligible. Additionally, the process may not be suitable for all equations, particularly those with complex or nonlinear behavior.
Detailed FAQs: Choose The Coefficient Closest To 0
What is the significance of coefficient values in equations?
Coefficient values determine the behavior of equations, influencing the shape and characteristics of their graphs. By altering coefficient values, we can manipulate the behavior of equations to suit specific requirements.
How do we approximate coefficients to zero?
Approximating coefficients to zero involves determining the coefficient value that is closest to zero without significantly altering the behavior of the equation. This can be achieved using various methods, such as rounding or using mathematical techniques.
What are the applications of approximating coefficients to zero in data analysis?
In data analysis, approximating coefficients to zero helps identify trends, patterns, and outliers in data sets. By removing insignificant coefficients, we can focus on the most influential factors and gain clearer insights into the data.