Lesson 1 Prime Factorization Answers presents a comprehensive guide to understanding prime factorization, a fundamental concept in number theory. This detailed exploration delves into the intricacies of prime numbers, common factors, and multiples, empowering readers with the knowledge to decompose any integer into its prime building blocks.

Through engaging explanations, practical examples, and real-world applications, this discourse unveils the significance of prime factorization in various fields, including cryptography, number theory, and modern technology. Embark on this journey of mathematical discovery and unlock the secrets of prime factorization.

Prime Factorization

Prime factorization is a fundamental concept in number theory that involves expressing a given integer as a product of prime numbers. A prime number is a positive integer greater than 1 that has no positive divisors other than 1 and itself.

Prime factorization provides a unique representation of an integer as a multiplication of its prime factors.

Steps in Prime Factorization

To perform prime factorization, follow these steps:

1. Repeatedly divide the given integer by the smallest prime number that divides it without leaving a remainder.
2. Continue dividing by prime numbers until the result is 1.
3. The factors obtained from each division are the prime factors of the original integer.

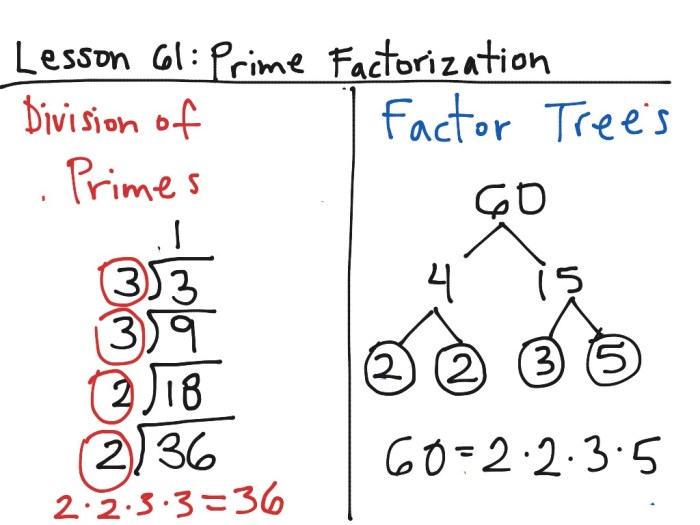
For example, to prime factorize 12:

• 12 ÷ 2 = 6
• 6 ÷ 2 = 3
• 3 ÷ 3 = 1

Therefore, the prime factorization of 12 is 2 × 2 × 3.

Prime Numbers

Prime numbers are positive integers greater than 1 that have exactly two distinct positive divisors: 1 and the number itself. Prime numbers are essential building blocks in number theory and have numerous applications in various fields.

Characteristics of Prime Numbers

Prime numbers possess several unique characteristics:

• The only even prime number is 2.
• Every other prime number is odd.
• The sum of two prime numbers is either prime or one less than a prime.
• The product of two prime numbers is always an odd number.
• There are infinitely many prime numbers.

Significance of Prime Numbers in Mathematics, Lesson 1 prime factorization answers

Prime numbers play a crucial role in various mathematical concepts, including:

• Unique Factorization Theorem:Every positive integer can be uniquely factored into a product of prime numbers.
• Modular Arithmetic:Prime numbers are used to define modular arithmetic, which has applications in cryptography and computer science.
• Number Theory:Prime numbers are central to many unsolved problems in number theory, such as the Goldbach conjecture and the twin prime conjecture.

Common Factors and Multiples

In mathematics, common factors and common multiples are essential concepts that help us understand the relationships between numbers. These concepts are widely used in various mathematical operations, including finding the greatest common factor (GCF) and the least common multiple (LCM) of two or more numbers.

Common Factors

Common factors are numbers that divide evenly into two or more numbers without leaving a remainder. For example, 2 is a common factor of 12 and 18 because it divides evenly into both numbers (12 ÷ 2 = 6, 18 ÷ 2 = 9).

To find the common factors of two or more numbers, we can use prime factorization. Prime factorization involves expressing a number as a product of prime numbers. The prime numbers that appear in the prime factorization of two or more numbers are the common factors of those numbers.

For example, the prime factorization of 12 is 2 × 2 × 3, and the prime factorization of 18 is 2 × 3 × 3. The common factors of 12 and 18 are 2 and 3, which are the prime numbers that appear in both prime factorizations.

Least Common Multiple (LCM): Lesson 1 Prime Factorization Answers

The least common multiple (LCM) of two or more integers is the smallest positive integer that is divisible by all of the given integers.

For example, the LCM of 2, 3, and 4 is 12, because 12 is the smallest positive integer that is divisible by 2, 3, and 4.

The LCM of two or more integers can be found by prime factorization. To find the LCM of two or more integers, first prime factorize each integer. Then, find the product of the highest powers of each prime factor that appears in any of the prime factorizations.

For example, to find the LCM of 2, 3, and 4, we first prime factorize each integer:

• 2 = 2
• 3 = 3
• 4 = 2 ²

The highest power of 2 that appears in any of the prime factorizations is 2 ². The highest power of 3 that appears in any of the prime factorizations is 3 ¹. Therefore, the LCM of 2, 3, and 4 is 2 ²– 3 ¹= 12.

Greatest Common Factor (GCF)

The Greatest Common Factor (GCF) of two or more numbers is the largest factor that divides all the numbers without leaving a remainder. It is also known as the Highest Common Factor (HCF).To find the GCF of two or more numbers, we can use the following steps:

• Find the prime factorization of each number.
• Identify the common prime factors and their lowest powers.
• Multiply the common prime factors with the lowest powers to get the GCF.

Relationship between GCF and Prime Factorization

The GCF of two or more numbers is related to their prime factorization. The GCF is the product of the common prime factors with the lowest powers. For example, the GCF of 12 and 18 is 6, which is the product of the common prime factor 2 with the lowest power 1.

Applications of Prime Factorization

Prime factorization is a fundamental concept in mathematics with wide-ranging applications in various fields. It provides a powerful tool for solving complex problems and understanding the underlying structure of numbers.

In this section, we will explore some of the key applications of prime factorization in real-world scenarios, including its significance in cryptography, number theory, and modern technology.

Cryptography

Prime factorization plays a crucial role in modern cryptography, the science of securing communication. It is used as the basis for many encryption algorithms, such as the widely used RSA algorithm. The RSA algorithm relies on the difficulty of factoring large numbers into their prime factors to ensure the security of encrypted messages.

Number Theory

Prime factorization is central to number theory, the study of the properties of integers. It is used to solve problems related to divisibility, greatest common factors (GCFs), and least common multiples (LCMs). Prime factorization also helps in understanding the distribution of prime numbers and other number-theoretic concepts.

Modern Technology

Prime factorization finds applications in various areas of modern technology. For example, it is used in:

• Computer science for data compression and error correction.
• Physics for analyzing the properties of materials and understanding atomic and molecular structures.
• Medicine for developing new drugs and understanding genetic sequences.

Common Queries

What is prime factorization?

Prime factorization is a process of expressing a given integer as a product of prime numbers.

How do I find the prime factorization of a number?

To find the prime factorization of a number, repeatedly divide the number by the smallest prime number that divides it until you reach a prime number.

What are the applications of prime factorization?

Prime factorization has applications in cryptography, number theory, and other fields where understanding the structure of numbers is crucial.